Liczba π i o co tyle szumu?
Święto liczby π 2021
odbędzie się w Centrum Nauki i Techniki EC1
👉 w dniach 9-14 marca 👈

O liczbie π słyszeli wszyscy. Jest to jedna z nieskończonego zbioru liczb, pojawiająca się jako stała we wzorach matematycznych i wzorach innych dyscyplin; wszędzie tam, gdzie używa się funkcji trygonometrycznych lub gdzie po prostu mierzy się koła, okręgi, elipsy lub inne figury zbliżone kształtem do wymienionych. Niektórzy pamiętają ze szkoły, że π jest ilorazem obwodu i średnicy dowolnego koła oraz że iloraz ten zawsze wynosi tyle samo, niezależnie od rozmiarów koła. Prawie każdy wie też, że π jest równa (w przybliżeniu) 3,14, ale nie każdy pamięta, że π jest liczbą, której cyfry układają się po przecinku jeszcze dalej, w nieregularny sposób i że chaotyczny na pozór, a przecież precyzyjnie i jednoznacznie wyznaczony, ciąg tych cyfr nigdy się nie kończy. W matematyce takie liczby jak π noszą nazwę niewymiernych i jest ich znacznie więcej niż liczb wymiernych, które są zawsze stosunkami liczb całkowitych. O liczbie π napisano wiele książek i artykułów, w których przytacza się mnóstwo anegdot z nią związanych i przykładów zastosowania. Skąd taka popularność π? Czemu ma służyć szum wokół niej?

Jako stosunek obwodu do średnicy π znana jest od około 4 tysięcy lat, ale prawdziwą sławę i rozgłos naszej bohaterce przyniosła irracjonalna pogoń wielu zwariowanych matematyków XVIII wieku, z Ludolphem van Ceulenem na czele, za kolejnymi cyframi jej rozwinięcia. Był wśród nich także William Johnes, dzięki któremu w 1706 roku powszechnie dziś używany znak „ludolfiny” (π) wszedł do obiegu, Izaakowi Newtonowi i Leonhardowi Eulerowi zaś przypisuje się rozpropagowanie tego znaku i dodatkowo jeszcze wyposażenie innych w użyteczne wzory, które, przy odrobinie cierpliwości i zdolnościach rachunkowych, nie wykraczających poza umiejętności ucznia dzisiejszej VI klasy szkoły podstawowej, przyczyniały się do odkrywania światu kolejnych, nie znanych wcześniej i nikomu niepotrzebnych cyfr po przecinku bohaterki tego artykułu. Prawdopodobnie to właśnie przeróżne dramatyczne zdarzenia towarzyszące temu wyścigowi oraz fale emocji wywołane współzawodnictwem matematyków, wycieńczeniem i zgonami zawiedzionych poszukiwaczy coraz dokładniejszej wartości π, spowodowały, że liczba ta zyskała tak duży rozgłos. Wydaje się, że bardziej od samej liczby π fascynująca jest sama fascynacja tą liczbą. Nie sądzę, żeby wielu współczesnych matematyków szczerze doceniało jej znaczenie dla rozwoju swojej dziedziny, za to większość prawdopodobnie traktuje ją z dużym przymrużeniem oka.
Z całą pewnością jednak wszyscy matematycy doceniają błyskotliwe piękno niektórych epifanii π, jak na przykład w słynnym wzorze Eulera z 1748 roku:
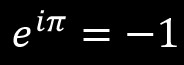
w którym π ukazuje się w pełnej krasie w towarzystwie innej, nie aż tak słynnej, liczby niewymiernej e oraz liczby urojonej i, którą otrzymano po wyciągnięciu pierwiastka kwadratowego z minus jedynki, co wielu nieobeznanych z liczbami zespolonymi uczniów uzna za herezję. Liczby π, e i i, połączone są we wzorze Eulera prostą zależnością, która może zachwycić tym, że wynik potęgowania liczby niewymiernej przy urojonym wykładniku z udziałem liczby π jest liczbą całkowitą ujemną. Jak to możliwe, że widzimy minus po prawej stronie znaku równości, a nie widzimy go po lewej, chociaż musi tam być? Tyle „niewymierności” po lewej prowadzi do „całkowitości” po prawej stronie? Nie bardzo trudne i niezbyt długie wyprowadzenie tego wzoru poleca się uczniom klas o profilu matematycznym.
 Zachwyt przytoczoną wyżej prawidłowością, obserwowany u matematyków wiele o nich mówi humanistom. Wywołuje czasem lekki grymas lekceważenia, warto jednak wtedy przypomnieć humanistom, że paru wybitnych twórców z ich grona zachwycało się liczbą π. Są wśród nich Umberto Eco, autor „Wahadła Foucaulta” i Wisława Szymborska, autorka wiersza „Liczba π”.
Zachwyt przytoczoną wyżej prawidłowością, obserwowany u matematyków wiele o nich mówi humanistom. Wywołuje czasem lekki grymas lekceważenia, warto jednak wtedy przypomnieć humanistom, że paru wybitnych twórców z ich grona zachwycało się liczbą π. Są wśród nich Umberto Eco, autor „Wahadła Foucaulta” i Wisława Szymborska, autorka wiersza „Liczba π”.
Istnieje kilka przesądów dotyczących liczby π, które powinno się obalać przy takiej okazji. Wspomnę o jednym. Wielu ludzi uważa, że skoro we wzorze na pole koła i obwód okręgu występuje liczba π, to zarówno pole jak i obwód zawsze muszą być liczbami niewymiernymi. Pogląd ten zakłada, że promień koła i druga potęga promienia muszą być liczbami wymiernymi. Założenie to nie jest prawdziwe, co łatwo uzasadnić podając odpowiednie przykłady.
O co zatem tyle szumu wokół liczby π? Uważni czytelnicy tego artykułu już się zapewne domyślili. Chodzi po prostu o to, by korzystając ze szczególnej reputacji tej liczby przypomnieć ludziom, którzy na co dzień nie zastanawiają się nad tym, jak ważna jest matematyka w naszym życiu i że warto uczyć się przedmiotów ścisłych. Ten cel usprawiedliwia wiele, na pierwszy rzut oka, dziwnych działań, między innymi takie wydarzenia jak obchody Dnia π, przypadające 14 marca, które niektórzy przedłużają nawet do tygodnia. Tak jak my, bo tegoroczne Święto Liczby PI w Centrum Nauki i Techniki EC1 potrwa od 9 do 14 marca 2021 r.
Marek Pisarski
Przeczytaj również: Gdzie i dlaczego szukać matematyki w Centrum Nauki EC1?




